Wartości funkcji: dodatnie, ujemne, nieujemne, niedodatnie
Funkcja przyjmuje wartości:
- dodatnie (f(x) > 0), gdy wykres funkcji znajduje się powyżej osi OX.
- ujemne (f(x) < 0), gdy wykres funkcji znajduje się poniżej osi OX.
- nieujemne (f(x) ⩾ 0), gdy wykres funkcji znajduje się powyżej osi OX lub ją
przecina. - niedodatnie (f(x) ⩽ 0), gdy wykres funkcji znajduje się poniżej osi OX lub ją
przecina.
Pozostało 84% treści
Zyskaj dostęp do setek lekcji przygotowanych przez ekspertów!
Wszystkie lekcje, fiszki, quizy, filmy i animacje są dostępne po zakupieniu subskrypcji.
W tej lekcji:
wartości funkcji dodatnie i ujemne
wartości funkcji nieujemne i niedodatnie
przykłady i zadania
Masz już dlaucznia.pl?
Zaloguj się
Miesięczny dostęp do wszystkich przedmiotów
- Dostęp do 9 przedmiotów
- Płatność co miesiąc
- Zrezygnuj kiedy chcesz!
Nie lubisz kupować kota w worku?
Sprawdź, jak wyglądają lekcje na Dla Ucznia
Dla Ucznia nauka zdalna liceum nauka zdalna portal
3:44
?
Co to znaczy?
przedział
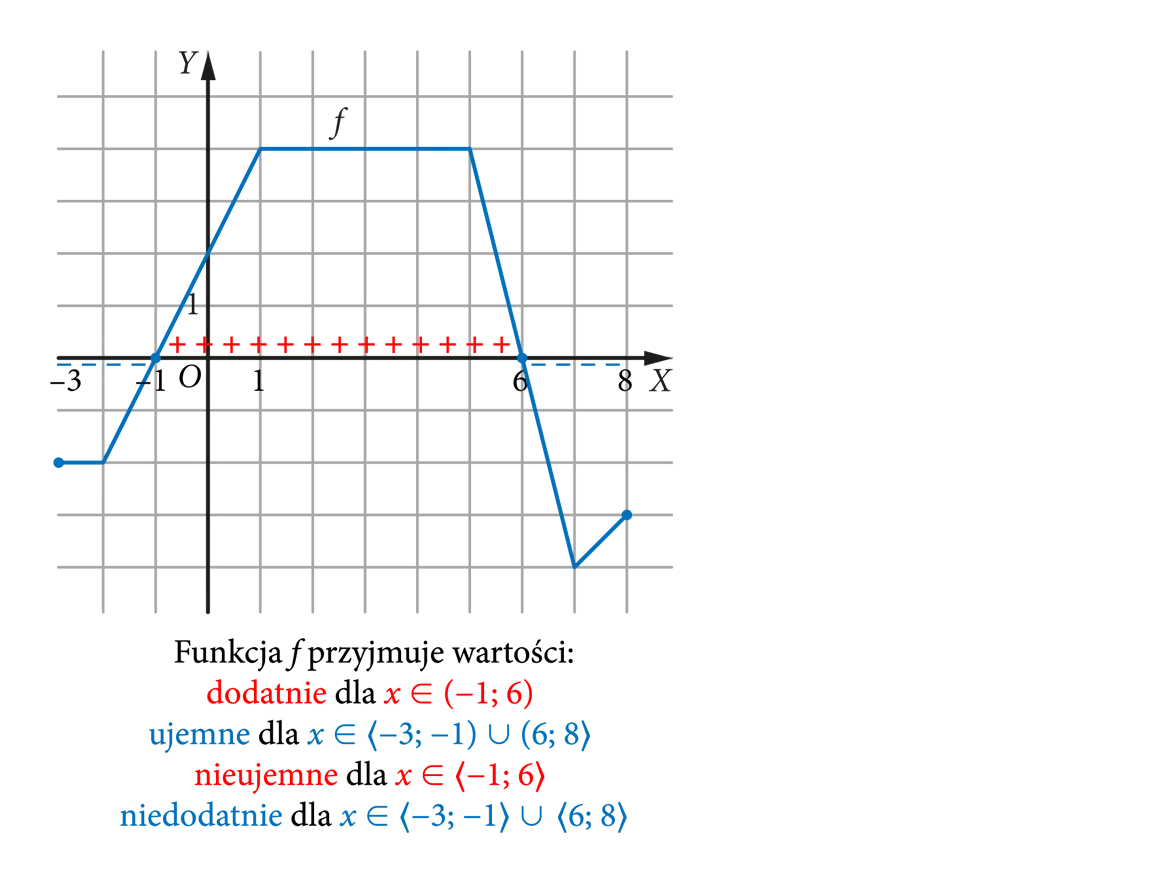
Przedział to podzbiór zbioru liczb rzeczywistych. Zapis (0; 2⟩ odpowiada przedziałowi, do którego
należą liczby większe od 0 i mniejsze lub równe 2.
należą liczby większe od 0 i mniejsze lub równe 2.