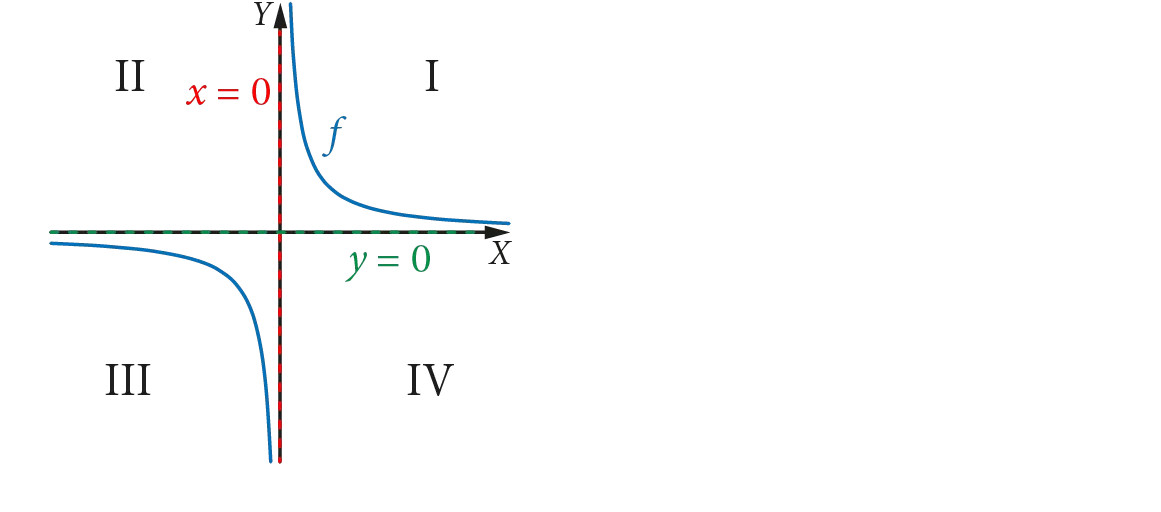dziedzina
Dziedzina funkcji (zbiór argumentów) to zbiór wszystkich liczb, dla których zostały określone wartości.
zbiór wartości
Zbiór wartości funkcji to zbiór tych liczb, które są wartościami dla argumentów funkcji.
funkcja jest malejąca
Funkcję nazywamy malejącą, jeśli dla dowolnych argumentów x1, x2, spełniony jest warunek:
jeśli x1 < x2, to f(x1) > f(x2)
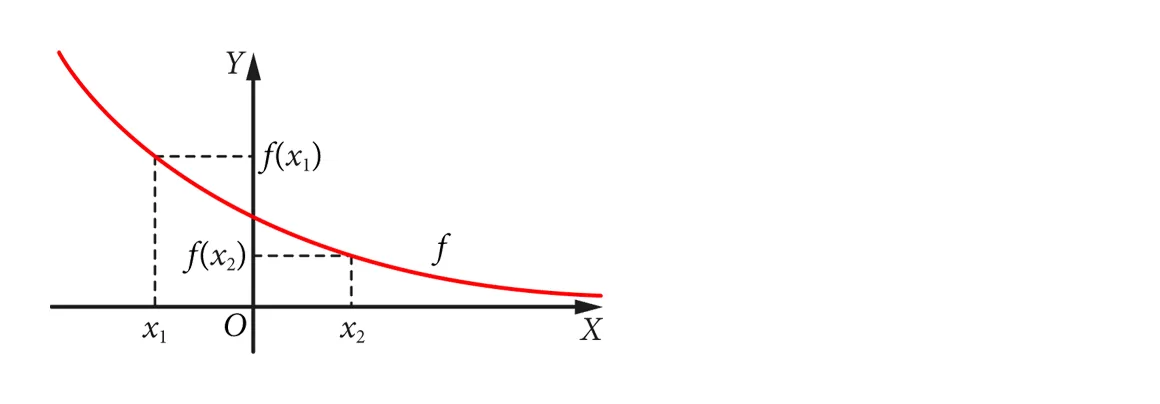
funkcja jest rosnąca
Funkcję nazywamy rosnącą, jeśli dla dowolnych argumentów x1, x2 spełniony jest warunek:
jeśli x1 < x2, to f(x1) < f(x2)
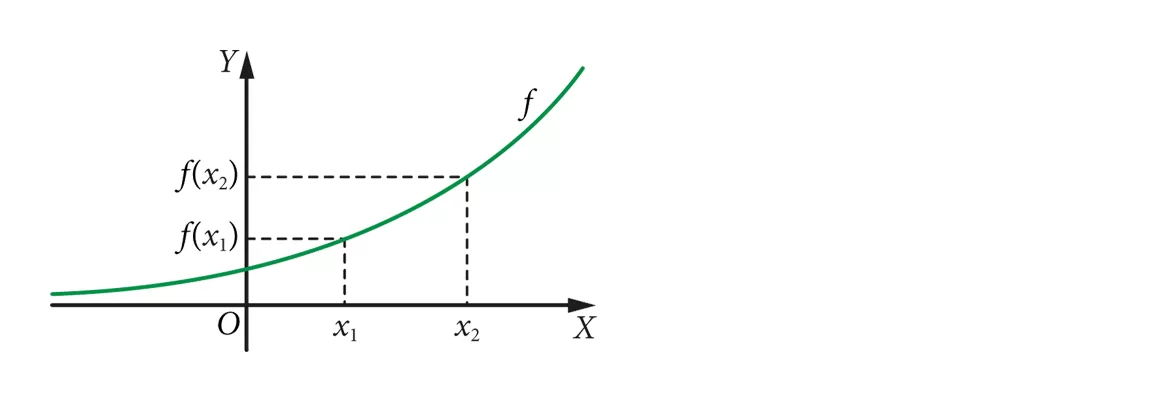
monotoniczność funkcji
Aby opisać monotoniczność funkcji, należy określić, czy jest ona: rosnąca, malejąca, stała, nierosnąca (malejąca lub stała) lub niemalejąca (rosnąca lub stała).
Funkcja może być niemonotoniczna w całej swojej dziedzinie.
Funkcja może być monotoniczna przedziałami.
jak narysować wykres funkcji
Aby narysować wykres funkcji, należy:
- ustalić kształt wykresu
- wyznaczyć kilka punktów należących do wykresu
- zaznaczyć punkty w układzie współrzędnych i poprowadzić przez nie krzywą
miejsce zerowe funkcji
Miejsce zerowe funkcji f jest to argument x, dla którego funkcja przyjmuje wartość 0.
f(x) = 0
Na przykład miejscem zerowym funkcji f (x)= 2x + 4 jest liczba x = −2, ponieważ f (−2)= 0.
stopień wielomianu
Stopień wielomianu zmiennej x to najwyższa potęga zmiennej x we wzorze wielomianu. Na przykład stopień wielomianu w(x) = 3x4 + x3 − 5x2 + 1 jest równy 4, co zapisujemy jako st (w) = 4.
Wielomianem stopnia pierwszego jest funkcja liniowa, np. g(x) = 5x + 2, st (g) = 1.
Wielomianem stopnia zerowego jest funkcja stała różna od 0, np. h(x) = 4, st (h) = 0.
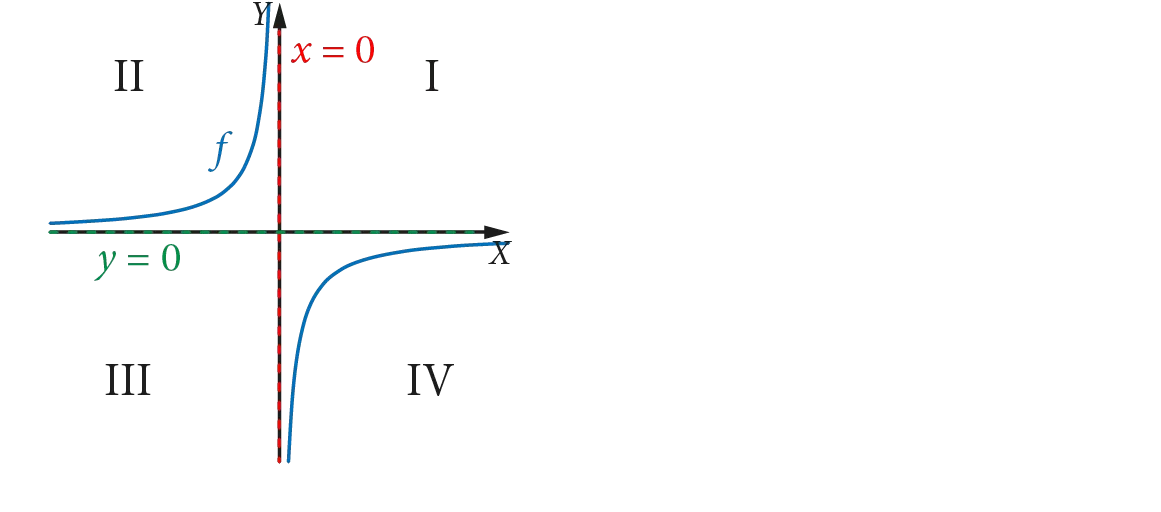
układ współrzędnych – numeracja ćwiartek
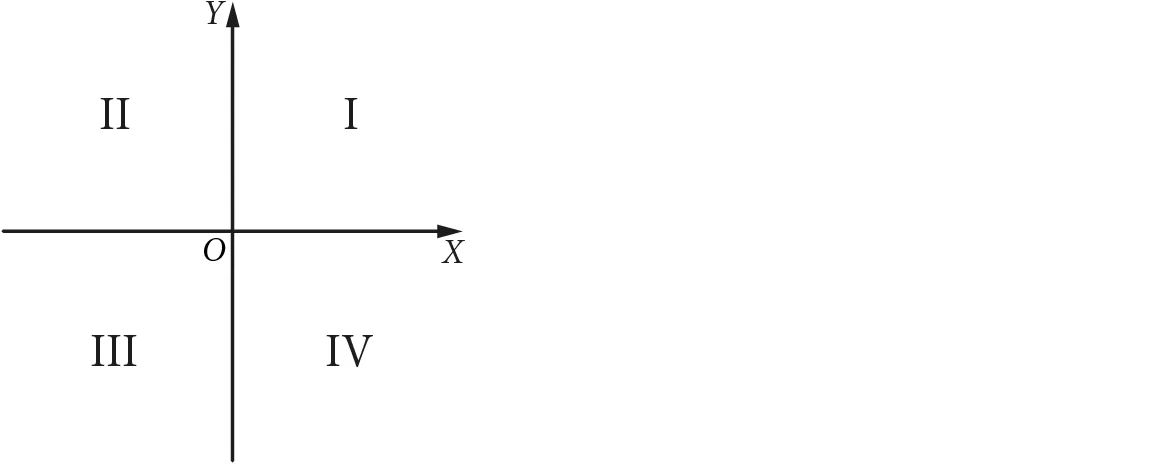
środek symetrii
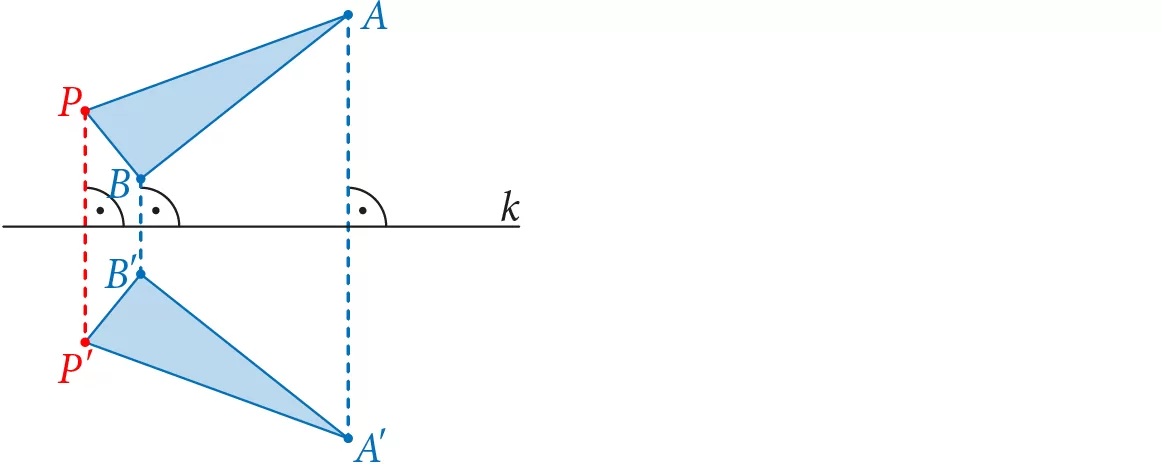
Symetria środkowa względem punktu O to przekształcenie, które punktowi P przyporządkowuje taki punkt P′, że punkty P, O, P′ leżą na jednej prostej oraz punkt O jest środkiem odcinka PP′. Punkt O nazywamy środkiem symetrii.
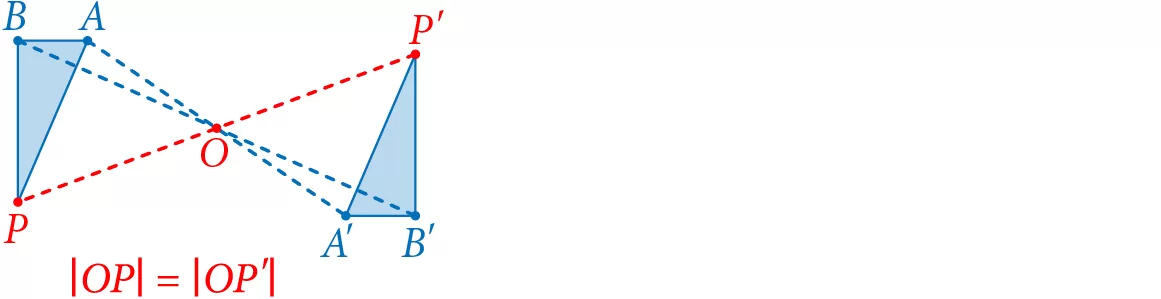
osie symetrii
Symetria osiowa względem prostej k to przekształcenie, które punktowi P przyporządkowuje taki punkt P′, że punkty P, P′ leżą na prostej prostopadłej do prostej k, po przeciwnych stronach prostej k, w takiej samej odległości od prostej k. Prostą k nazywamy osią symetrii.
punkty przecięcia wykresu z osiami OX i OY
Wykres funkcji przecina oś OX w punkcie o współrzędnych (x, 0).
Wykres funkcji przecina oś OY w punkcie o współrzędnych (0, y).
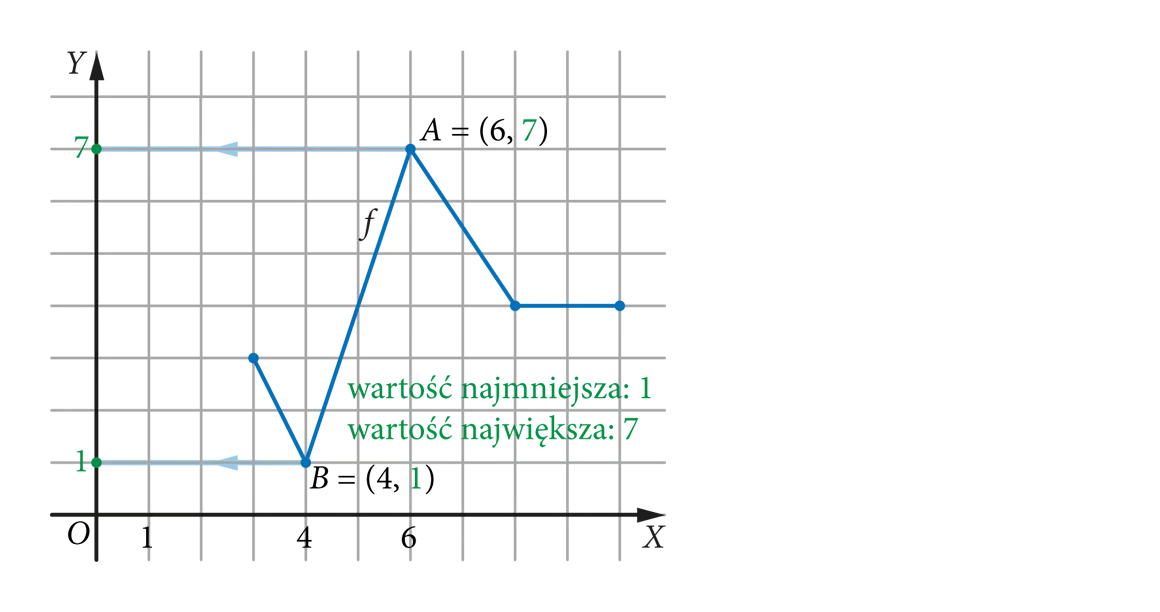
wartości największa i najmniejsza
Wartość najmniejsza funkcji odpowiada drugiej współrzędnej punktu, który na wykresie funkcji jest położony najniżej.
Wartość największa funkcji odpowiada drugiej współrzędnej punktu, który na wykresie funkcji jest położony najwyżej.
wartości dodatnie
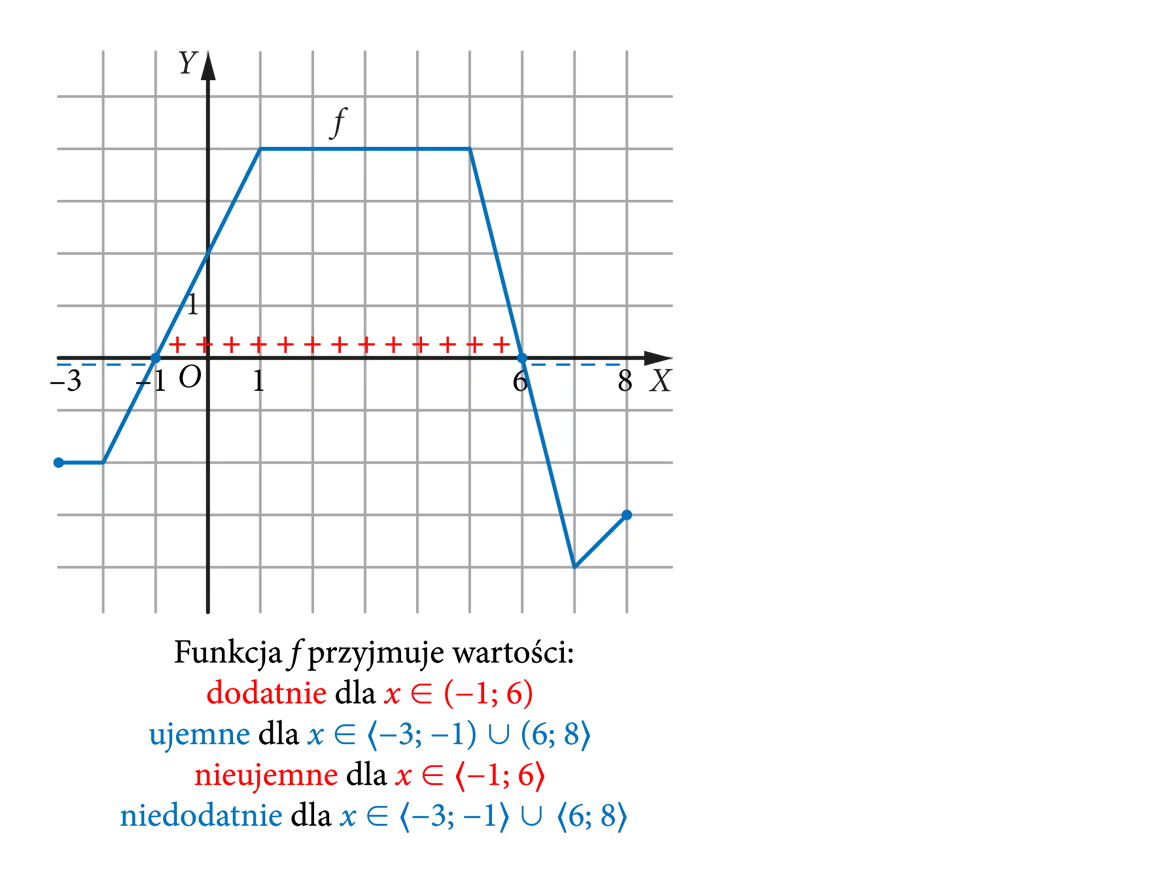
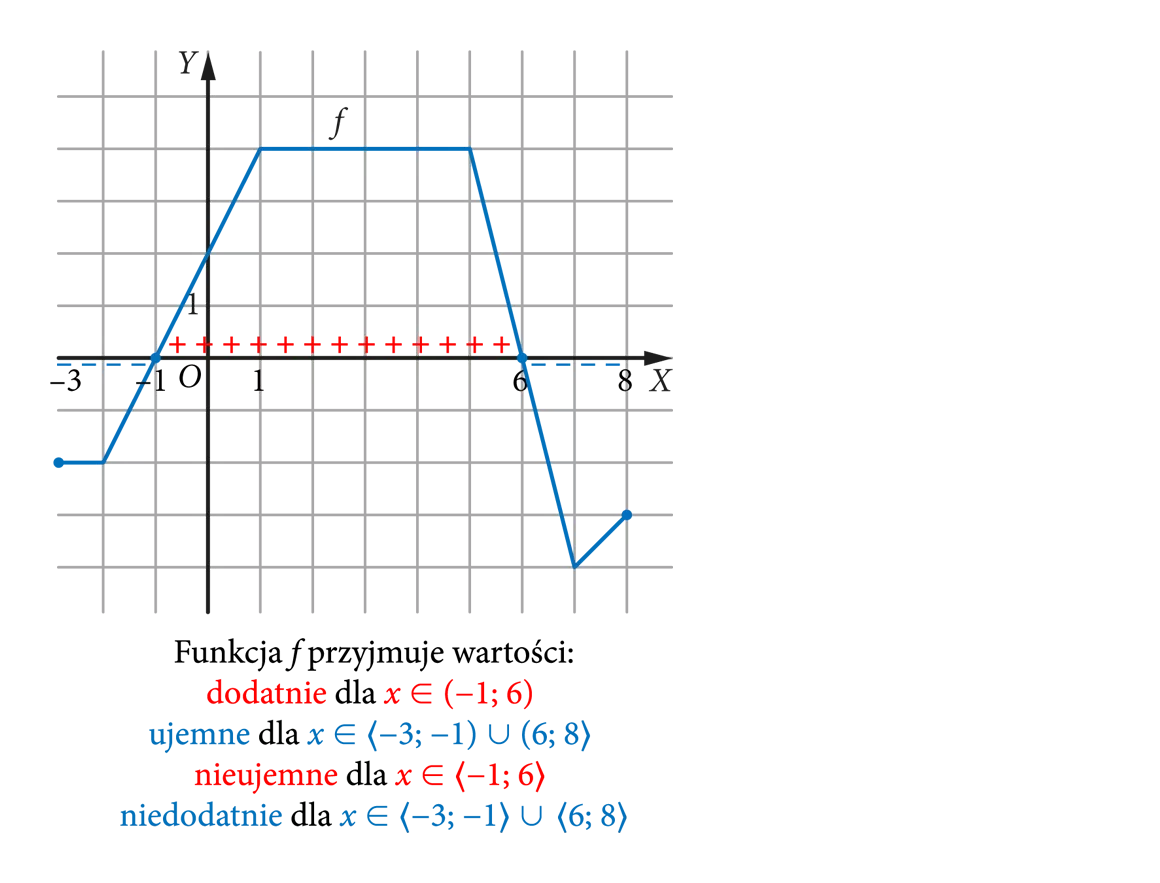
Funkcja przyjmuje wartości:
- dodatnie, gdy wykres funkcji znajduje się powyżej osi OX.
- ujemne, gdy wykres funkcji znajduje się poniżej osi OX.
- nieujemne, gdy wykres funkcji znajduje się powyżej osi OX lub ją przecina.
- niedodatnie, gdy wykres funkcji znajduje się poniżej osi OX lub ją przecina.
wartości ujemne
Funkcja przyjmuje wartości:
- dodatnie, gdy wykres funkcji znajduje się powyżej osi OX.
- ujemne, gdy wykres funkcji znajduje się poniżej osi OX.
- nieujemne, gdy wykres funkcji znajduje się powyżej osi OX lub ją przecina.
- niedodatnie, gdy wykres funkcji znajduje się poniżej osi OX lub ją przecina.