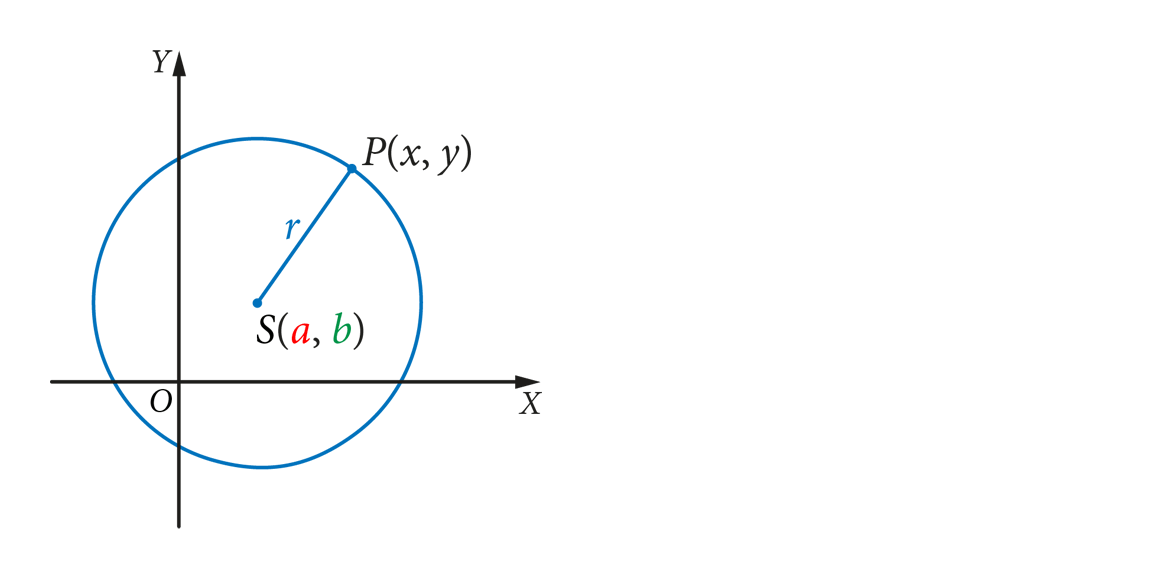Okrąg o środku w punkcieS\, \mleft(\textcolor{#E94D00}{a},\textcolor{#75A600}{b}\mright) S(a, b) i promieniu\textcolor{#005FD4}{r}\gt 0 r > 0 ma równanie:
\left(x-\textcolor{#E94D00}{a}\right)^2+\left(y-\textcolor{#75A600}{b}\right)^2=\textcolor{#005FD4}{r}^2 (x − a)2 + (y − b)2 = r2
Jest to równanie okręgu w postaci kanonicznej.
Przykłady
1. Okrąg o środku w punkcie\left(\textcolor{#E94D00}{0},\textcolor{#75A600}{0}\right) (0, 0) i promieniu\textcolor{#005FD4}{7} 7 ma równanie:
x^2+y^2=\textcolor{#005FD4}{7}^2\! , x2 + y2 = 72, czyli:
x^2+y^2=49 x2 + y2 = 49
2. Okrąg o środku w punkcie\left(\textcolor{#E94D00}{8},\textcolor{#75A600}{-2}\right) (8, −2) i promieniu\textcolor{#005FD4}{\sqrt{3}} √3 ma równanie:
\left(x-\textcolor{#E94D00}{8}\right)^2+\left(y-\left(\textcolor{#75A600}{-2}\right)\right)^2=\left(\textcolor{#005FD4}{\sqrt{3}}\right)^{\! 2}\! , (x − 8)2 + (y − (−2))2 = (√3)2, czyli:
\left(x-8\right)^2+\left(y+2\right)^2=3 (x − 8)2 + (y + 2)2 = 3
3. Punkt\left(\textcolor{#E94D00}{2},\textcolor{#75A600}{3}\right) (2, 3) należy do okręgu o równaniu\left(x-6\right)^2+y^2=25, (x − 6)2 + y2 = 25, ponieważ:
\left(\textcolor{#E94D00}{2}-6\right)^2+\textcolor{#75A600}{3}^2=25 (2 − 6)2 + 32 = 25