Twierdzenie odwrotne do twierdzenia Talesa

Twierdzenie odwrotne do twierdzenia Talesa

Twierdzenie odwrotne do twierdzenia Talesa brzmi następująco:

Jeżeli odcinki wyznaczone przez dwie proste na jednym ramieniu kąta (oznaczonym na rysunku jako 1) są proporcjonalne do odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu kąta (oznaczonym na rysunku jako 2), to proste te są równoległe.

Przykład

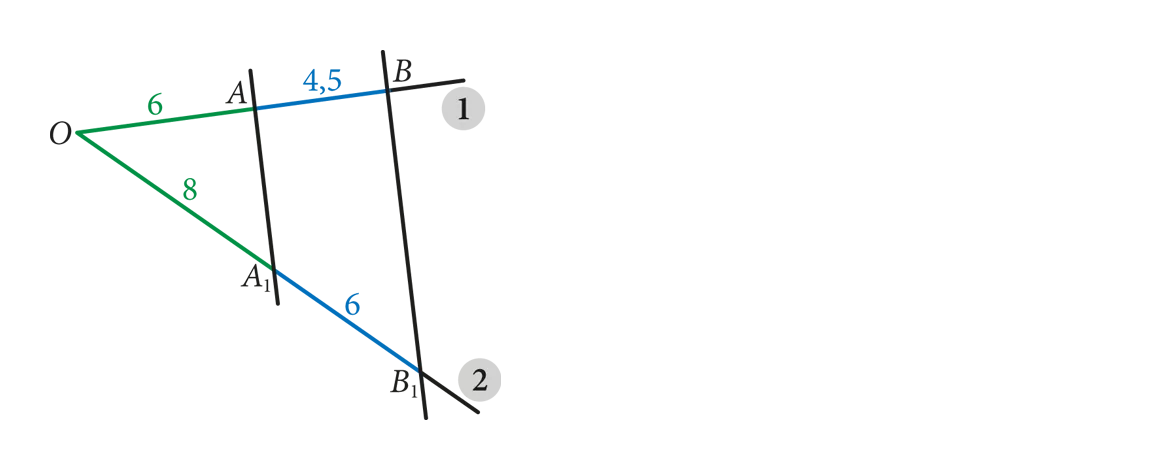
Stosunek odcinków zielonych jest równy stosunkowi odcinków niebieskich:
\textcolor{#75A600}{\frac{6}{8}}\textcolor{#000000}{=0,75} 68  =  0, 75 oraz\textcolor{#005FD4}{\frac{4,5}{6}}=0,75 4, 56  =  0, 75

Zachodzi zatem równość:
\frac{\left|OA\right|}{\left|\left.\mleft.OA\mright.\right._{\mleft.1\mright.}\right|}=\frac{\left|AB\right|}{\left|\left.A\right._{\mleft.1\mright.}B_{\mleft.1\mright.}\right|} ∣OA∣∣OA1∣  =  ∣AB∣∣A1B1∣

Stąd wynika, że prosteAA_1 AA1 iBB_{\mleft.1\mright.} BB1 są równoległe.