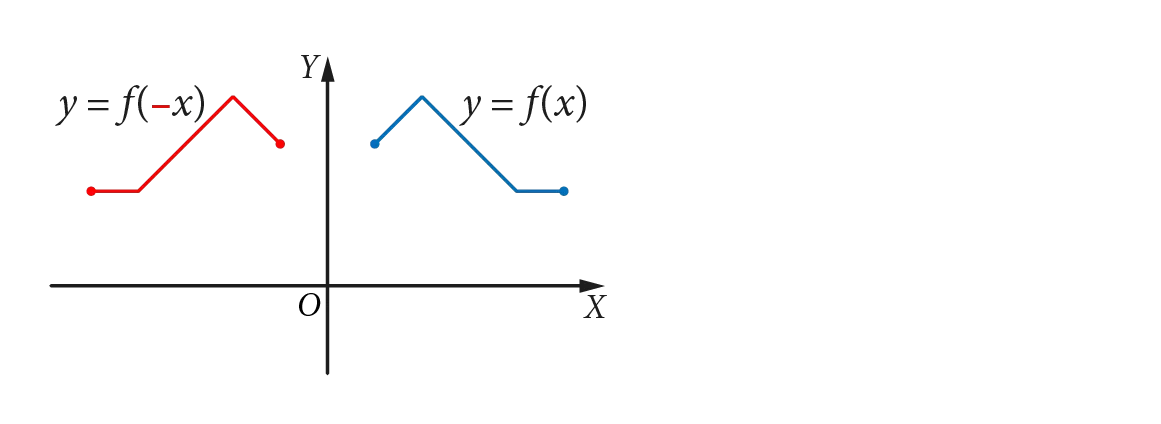Wyznaczanie współrzędnych punktu w symetrii względem osi OX i OY
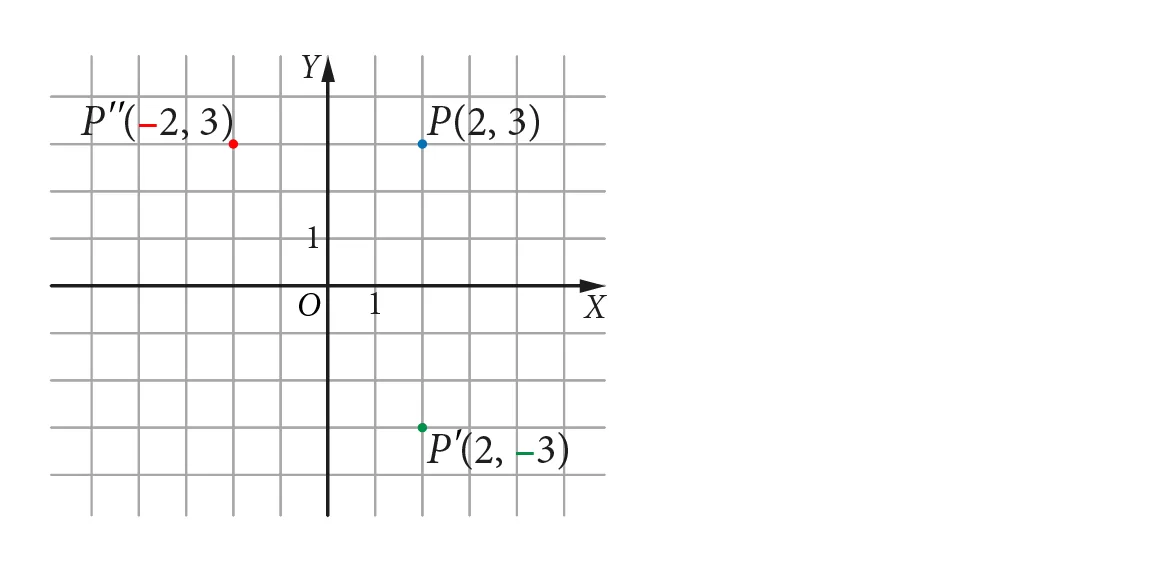
Poniżej znajduje się rysunek przedstawiający punkt P (2, 3), który został symetrycznie odbity względem osi OX i OY:

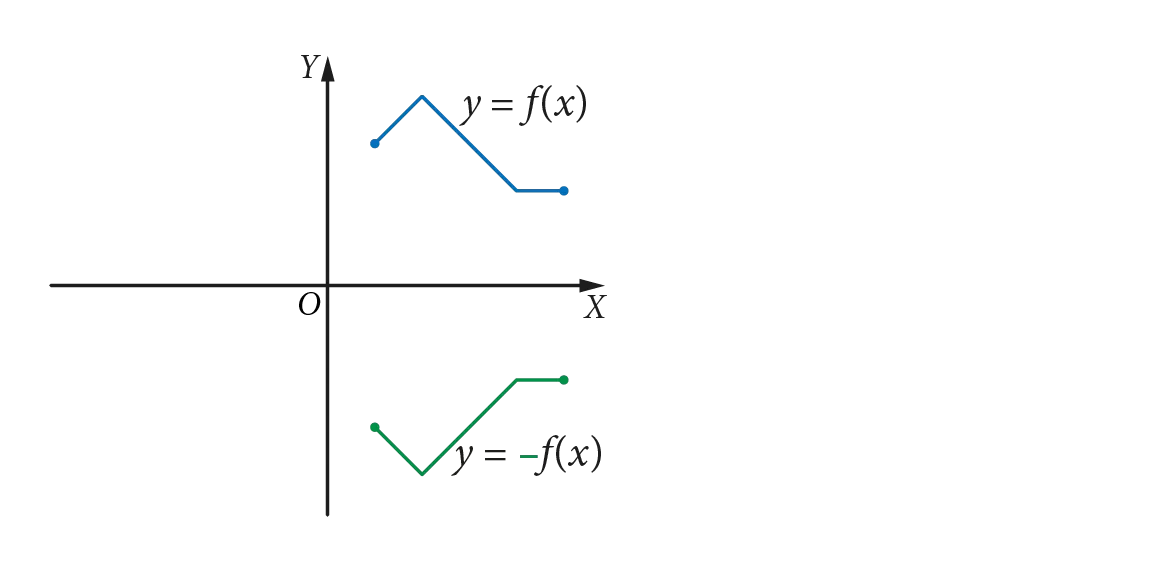
Symetria wykresu funkcji y = f(x) względem osi OX
Na rysunku znajdują się wykresy funkcji f(x) oraz g(x) = −f(x):
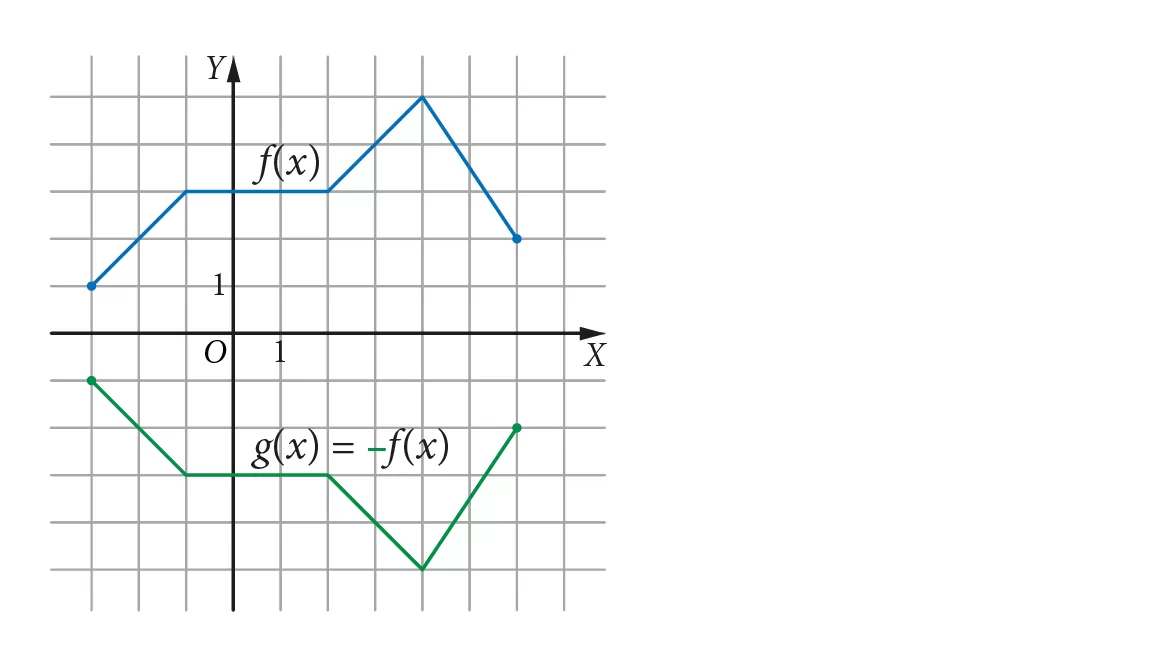
Wykres funkcji g(x) = −f(x) można otrzymać z wykresu funkcji f(x) przez symetryczne odbicie go względem osi OX.
- Funkcje f i g dla tych samych argumentów przyjmują wartości przeciwne, np. jeśli f(6) = 2, to g(6) = −2.
Inne przykłady wykresów funkcji f(x) oraz g(x) = −f(x)
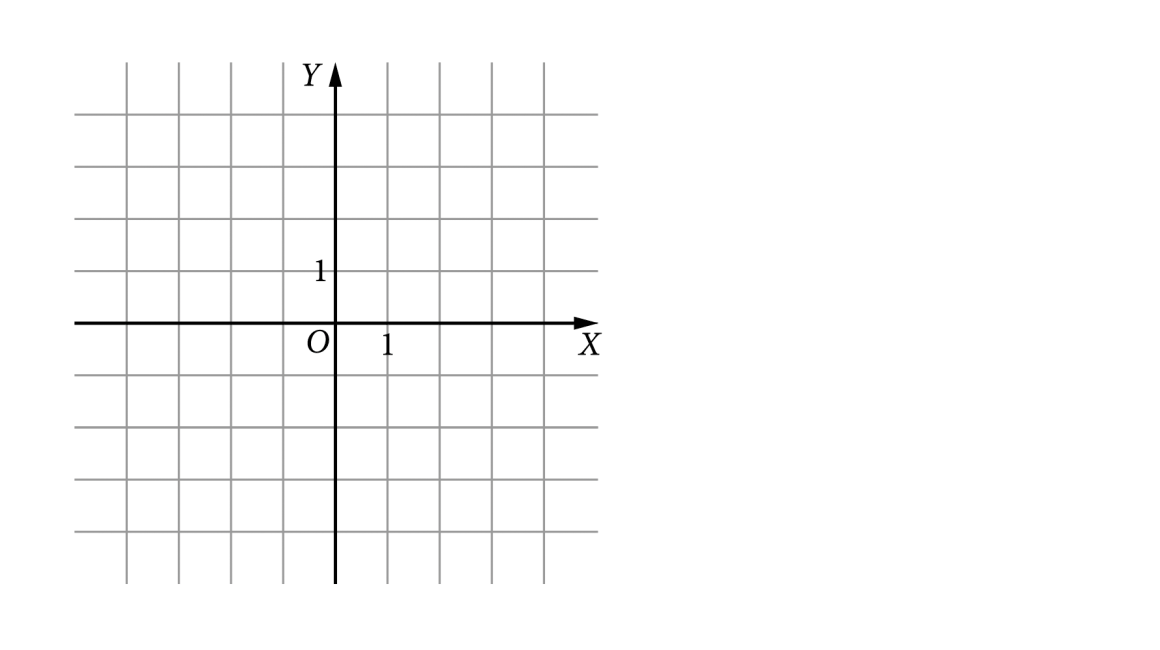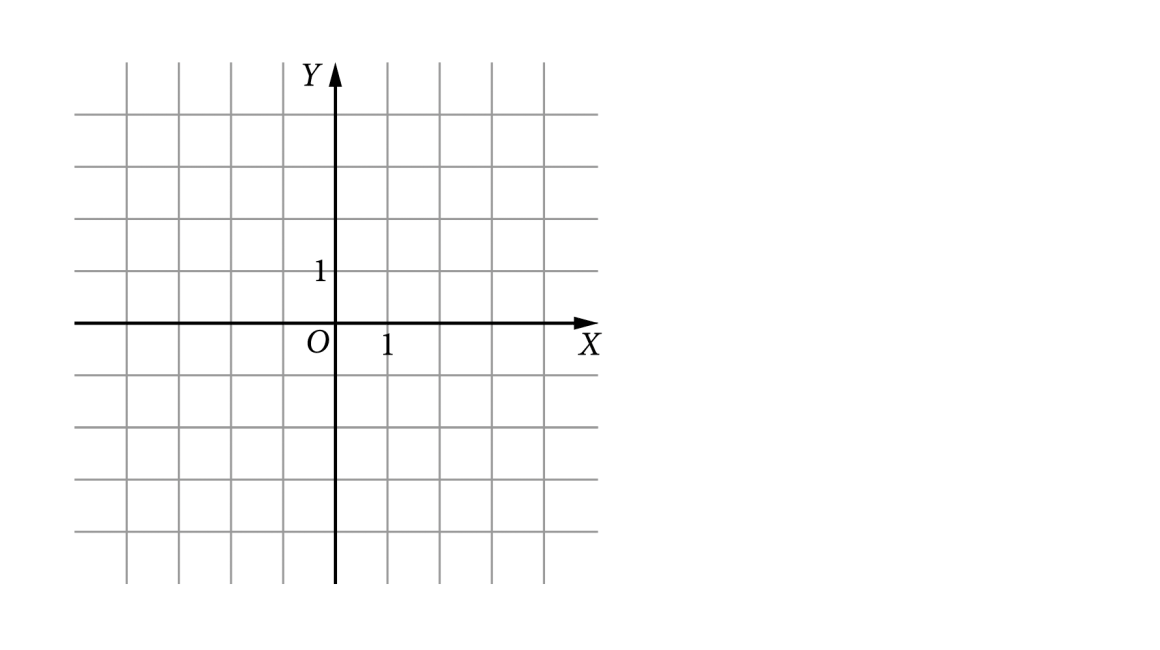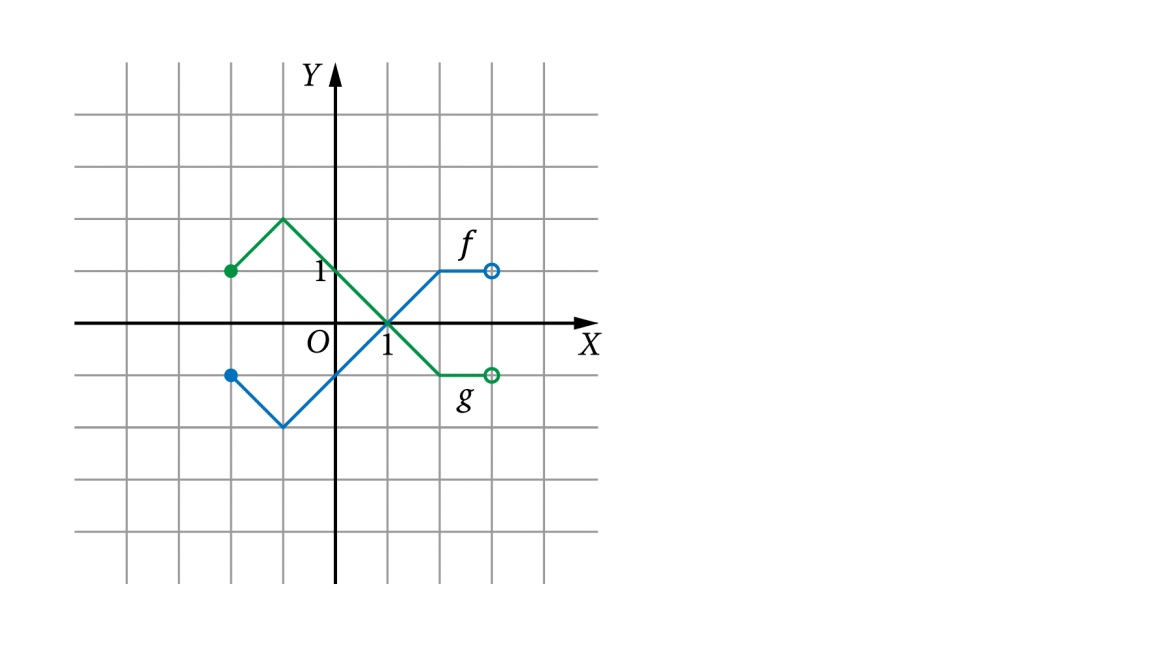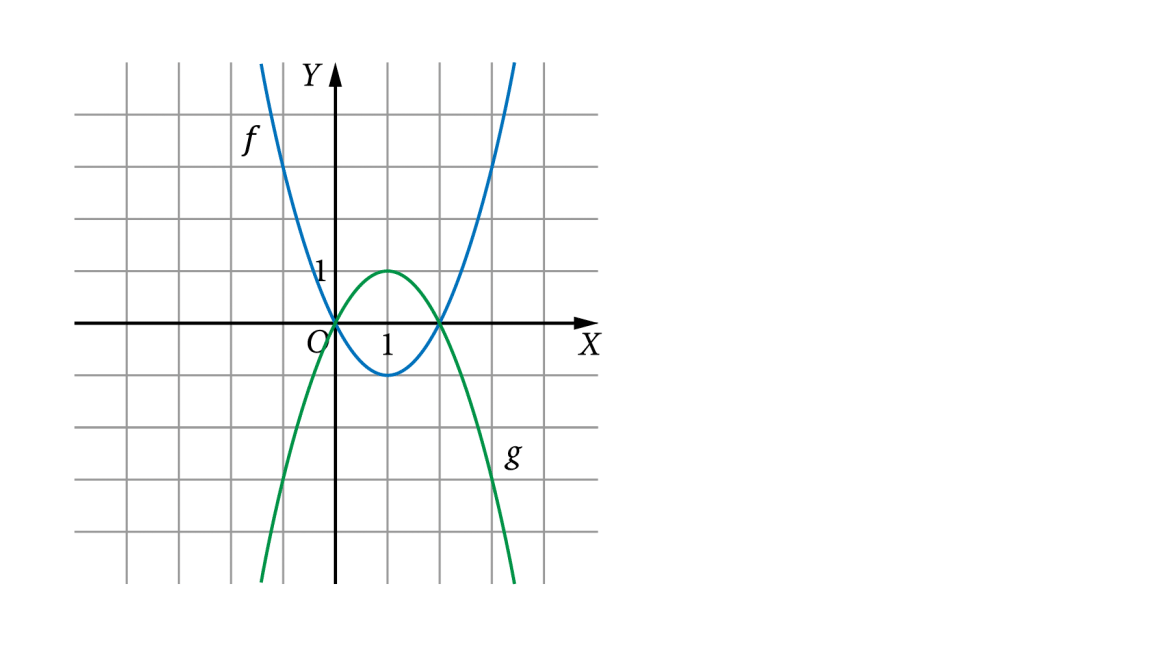
- Zauważ, że dziedziny funkcji f(x) oraz g(x) = −f(x) są takie same, natomiast zbiory wartości tych funkcji są różne.
Symetria wykresu funkcji y = f(x) względem osi OX a wzory różnych funkcji

Symetria wykresu funkcji f względem osi OY
Na rysunku znajdują się wykresy funkcji f(x) oraz g(x) = f(−x):
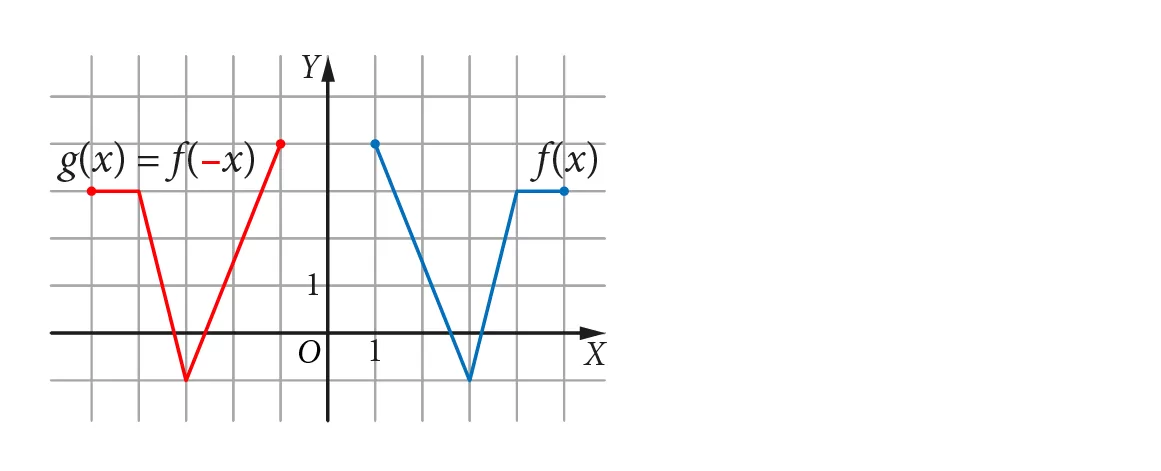
Wykres funkcji g(x) = f(−x) można otrzymać z wykresu funkcji f(x) przez symetryczne odbicie go względem osi OY.
- Funkcje f i g dla argumentów będących liczbami przeciwnymi przyjmują te same wartości, np. jeśli f(4) = 3, to g(−4) = 3.
Inne przykłady wykresów funkcji f(x) oraz g(x) = f(−x)
- Zauważ, że dziedziny funkcji f(x) oraz g(x) = f(−x) mogą być różne, natomiast zbiory wartości funkcji f i g są takie same.
Symetria wykresu funkcji y = f(x) względem osi OY a wzory różnych funkcji

- W przypadku funkcji y = 6x, y = x3 oraz y = 1x wzory otrzymane po odbiciu symetrycznym ich wykresów względem osi OY (y = −6x, y = −x3 oraz y = −1x) są takie same jak po ich odbiciu symetrycznym względem osi OX (y = −6x, y = −x3 oraz y = −1x).
- W przypadku funkcji y = √x dziedzina x ≥ 0 uległa zmianie, ponieważ liczba pod pierwiastkiem parzystego stopnia nie może być ujemna, czyli −x ≥ 0, skąd x ≤ 0.
Łączenie symetrii względem osi układu współrzędnych
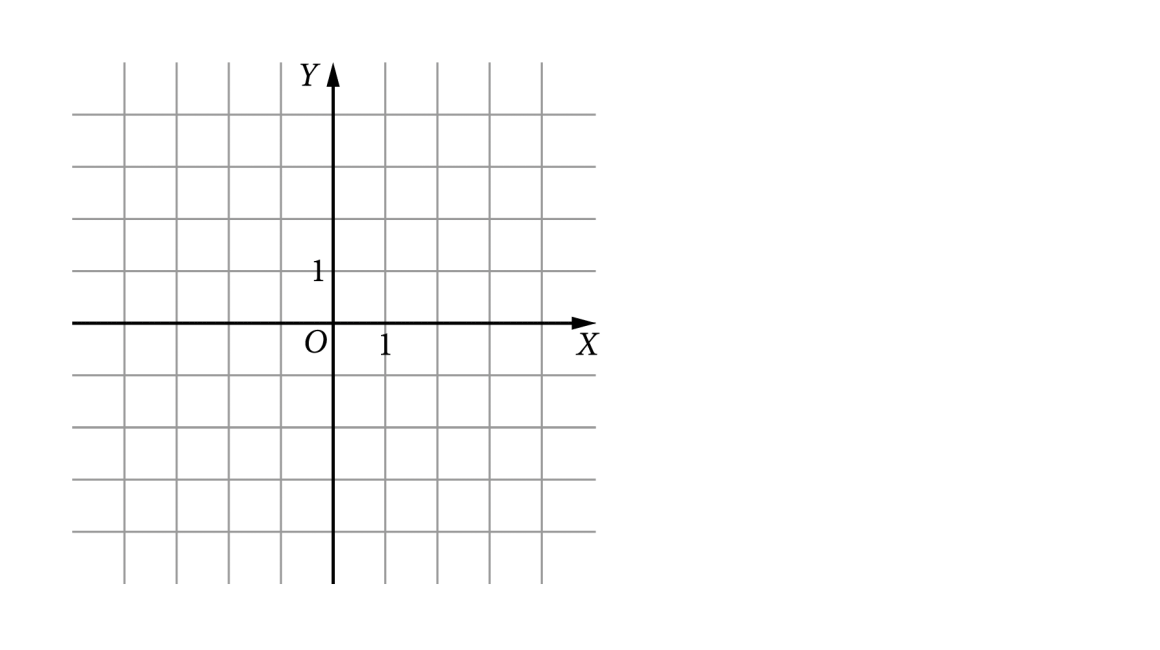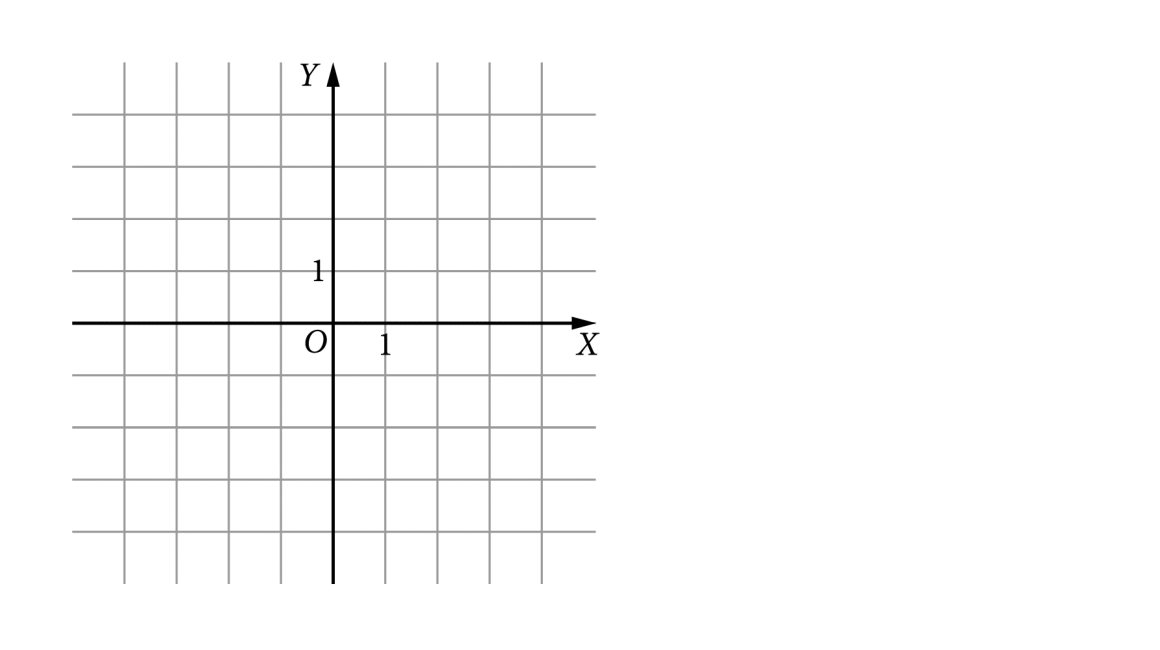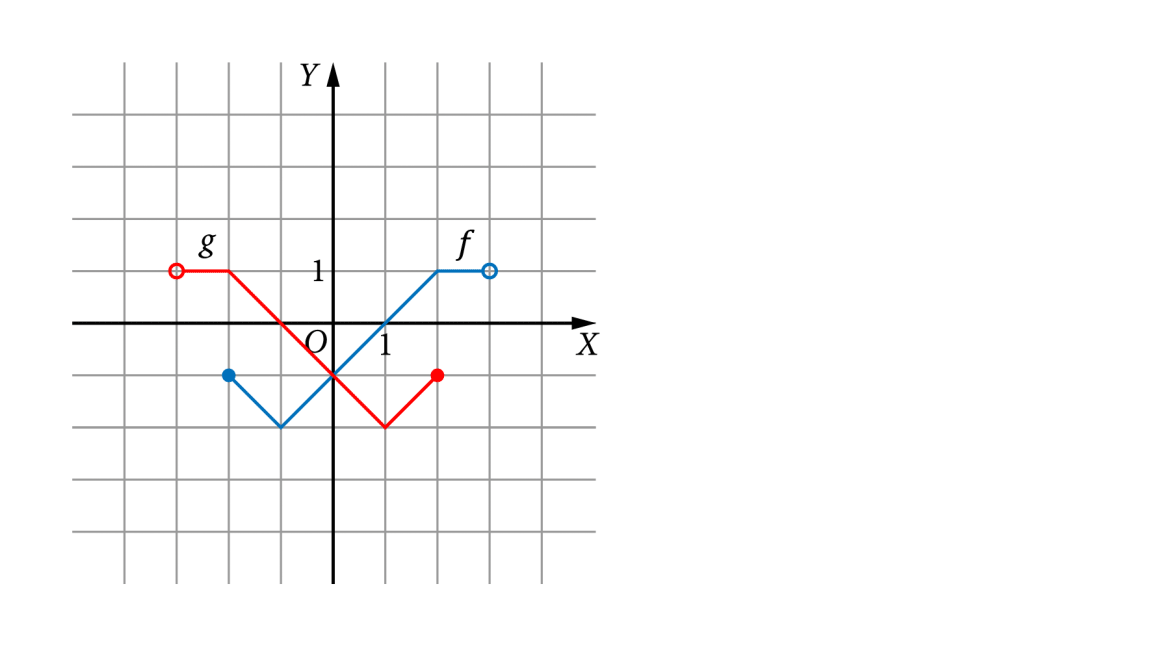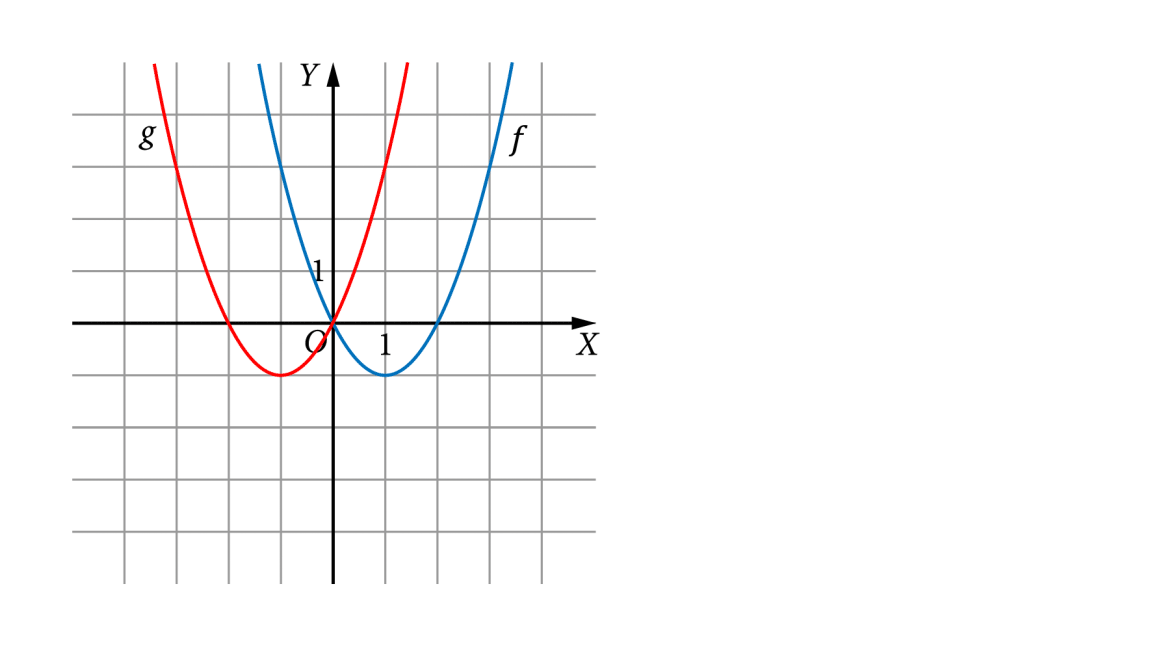
Symetrie względem osi układu współrzędnych można łączyć ze sobą, tj. wykonywać odbicia jedne po drugim. Na poniższym rysunku znajdują się wykresy funkcji f, g i h, takie, że:
● wykres funkcji g otrzymujemy przez odbicie symetryczne względem osi OX wykresu funkcji f, zatem g(x) = −f(x),
● wykres funkcji h otrzymujemy przez odbicie symetryczne względem osi OY wykresu funkcji g, zatem h(x) = g(−x). Wzór funkcji h możemy też zapisać w postaci: h(x) = g(−x) = −f(−x).
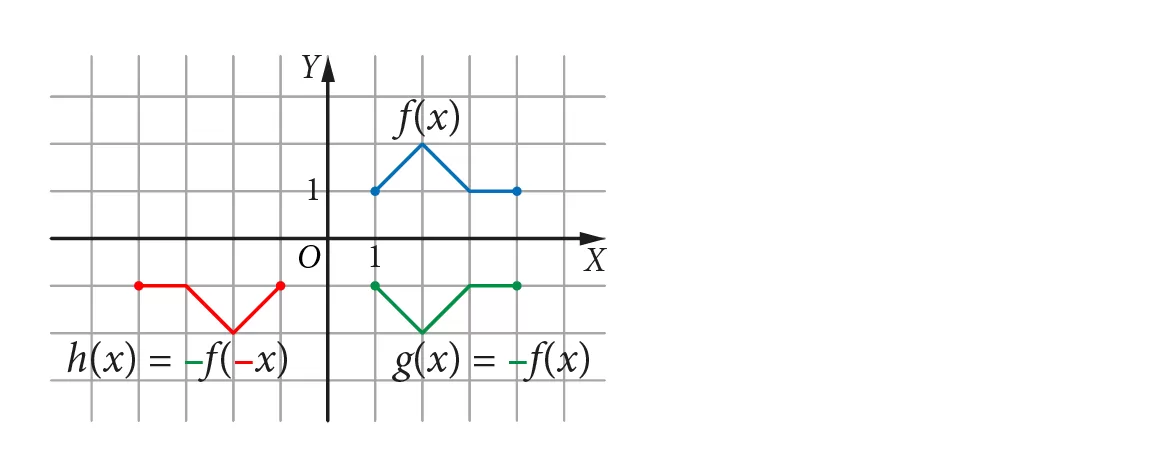
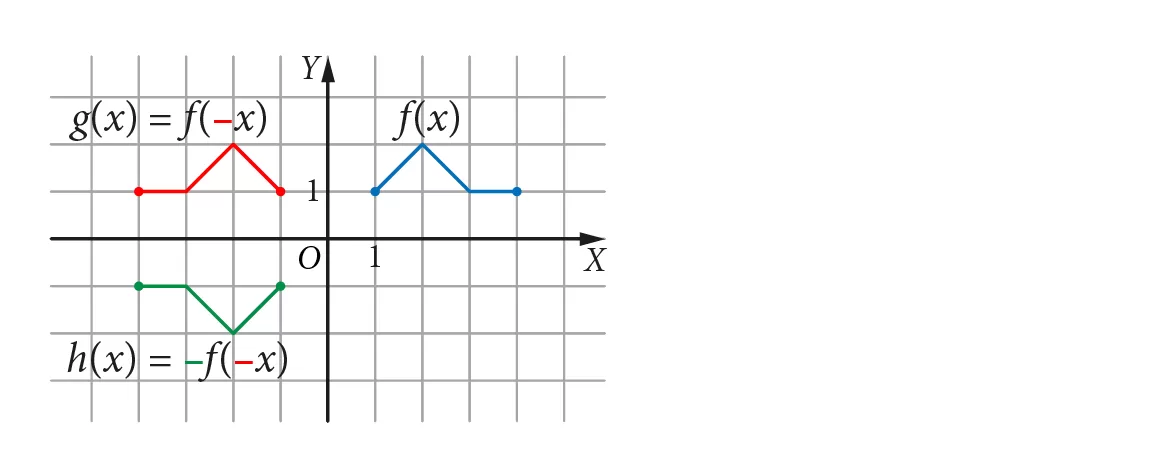
Jeśli zmienimy kolejność przekształceń, czyli wykres funkcji f odbijemy symetrycznie najpierw względem osi OY, a następnie otrzymany wykres względem osi OX, to wykres funkcji h pozostanie bez zmian.
● g(x) = f(−x),
● h(x) = −g(x) = −f(−x).
- Kolejność odbijania wykresów funkcji względem osi układu współrzędnych nie ma znaczenia dla wyniku końcowego.
- Przekształcenie polegające na wykonaniu dwóch symetrycznych odbić względem jednej osi układu współrzędnych, a następnie względem drugiej osi nazywamy symetrią środkową względem początku układu współrzędnych (punktu (0, 0)).
- Dziedziny i zbiory wartości funkcji f oraz h:

Łączenie symetrii a wzory różnych funkcji

Łączenie symetrii – zadania z rozwiązaniami
Zadanie 1. Dana jest funkcja f(x) = 5x − 9. Zapisz wzór funkcji otrzymanej po odbiciu symetrycznym wykresu funkcji f:
a) względem osi OX,
b) względem osi OY,
c) najpierw względem osi OX, następnie względem osi OY,
d) najpierw względem osi OY, następnie względem osi OX.
Rozwiązanie:
a) g(x) = −f(x) = −(5x − 9) = −5x + 9
b) g(x) = f(−x) = 5(−x) − 9 = −5x − 9
c) po odbiciu względem osi OX: g(x) = −f(x) = −5x + 9
następnie po odbiciu względem osi OY: h(x) = g(−x) = −5(−x) + 9 = 5x + 9
d) po odbiciu względem osi OY: g(x) = f(−x) = −5x − 9
następnie po odbiciu względem osi OX: h(x) = −g(x) = −(−5x − 9) = 5x + 9
- Kolejność wykonywania symetrii względem osi OX i OY nie ma znaczenia dla wyniku końcowego. W podpunktach c) i d) otrzymaliśmy taki sam końcowy wzór funkcji.
Zadanie 2. Dana jest funkcja f(x) = 2x2 + x − 1. Zapisz wzór funkcji otrzymanej po odbiciu symetrycznym wykresu funkcji f:
a) względem osi OX,
b) względem osi OY,
c) najpierw względem osi OX, następnie względem osi OY,
d) najpierw względem osi OY, następnie względem osi OX.
Rozwiązanie:
a) g(x) = −f(x) = −(2x2 + x − 1) =
= −2x2 − x + 1
b) g(x) = f(−x) = 2(−x)2 + (−x) − 1 =
= 2x2 − x − 1
c) po odbiciu względem osi OX: g(x) = −f(x) = −2x2 − x + 1
następnie po odbiciu względem osi OY: h(x) = g(−x) = −2(−x)2 − (−x) + 1 =
= −2x2 + x + 1
d) po odbiciu względem osi OY: g(x) = f(−x) = 2x2 − x − 1
następnie po odbiciu względem osi OX: h(x) = −g(x) = −(2x2 − x − 1) =
= −2x2 + x + 1
Łączenie symetrii i przesunięć – zadania z rozwiązaniami
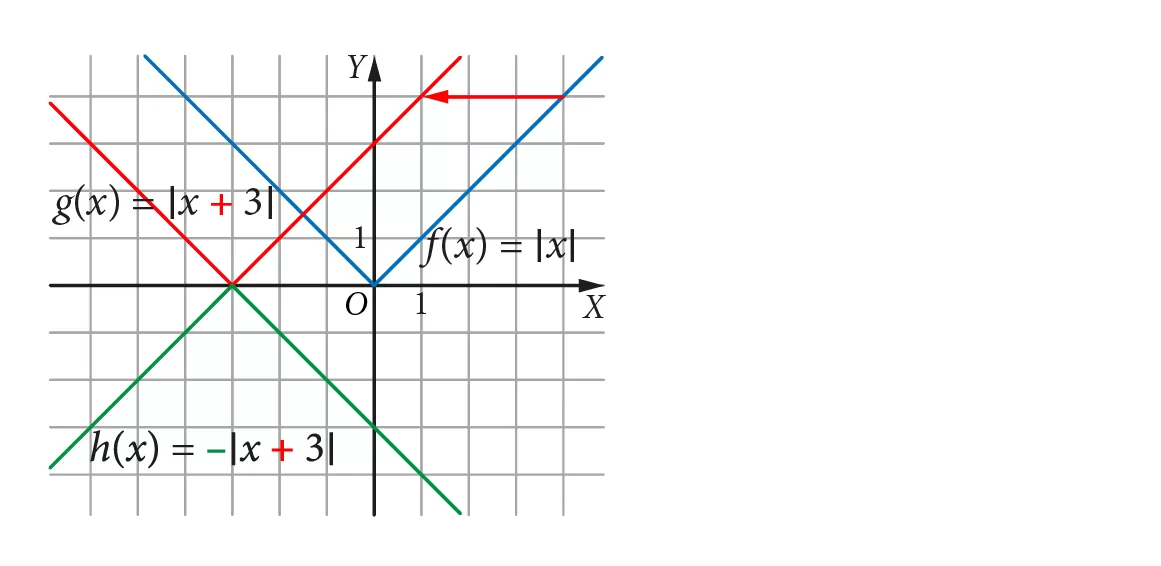
Zadanie 1. Naszkicuj wykres funkcji f(x) = ∣x∣, a następnie wykresy funkcji g(x) = f(x + 3), h(x) = −f(x + 3).
Rozwiązanie:
Krok 1. Szkicujemy wykres funkcji f(x) = ∣x∣.
Krok 2. Wykres funkcji g(x) = f(x + 3) = ∣x + 3∣ otrzymamy po przesunięciu wykresu funkcji f o 3 jednostki w lewo.
Krok 3. Wykres funkcji h(x) = −f(x + 3) = −∣x + 3∣ otrzymamy po odbiciu symetrycznym wykresu funkcji g względem osi OX.
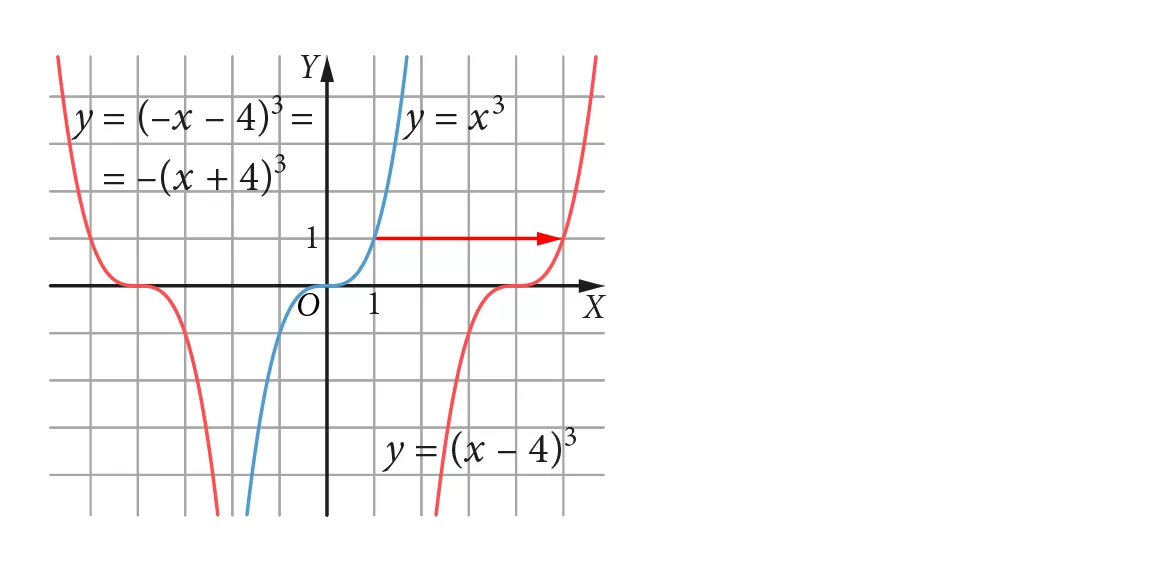
Zadanie 2. Na rysunku znajdują się wykresy funkcji określonych wzorami f(x) = x3, g(x) = (x − 4)3 oraz h(x) = −(x − 4)3. Dopasuj wykresy do odpowiednich wzorów.
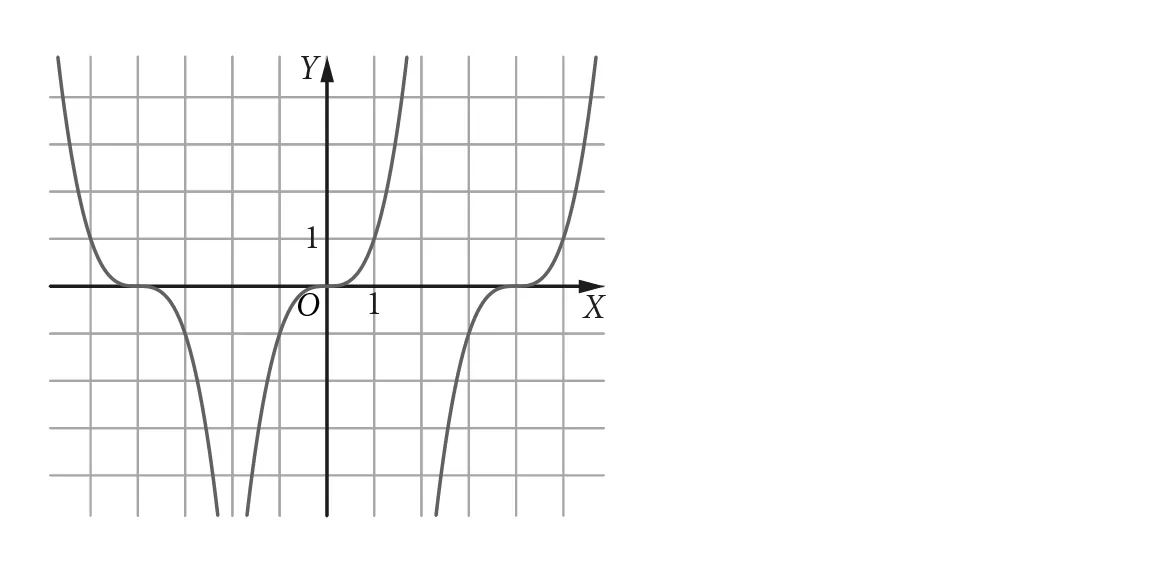
Rozwiązanie:
● Środkowy wykres to wykres funkcji f(x) = x3.
● Wykres po prawej stronie otrzymamy po przesunięciu wykresu funkcji f o 4 jednostki w prawo, czyli wykres funkcji f(x − 4). Będzie to zatem wykres funkcji g(x) = (x − 4)3.
● Wykres po lewej stronie otrzymamy po odbiciu symetrycznym względem osi OY wykresu funkcji g, czyli wykres g(−x). Będzie to zatem wykres funkcji h(x) = (−x − 4)3.
liczba przeciwna
Aby wyznaczyć liczbę przeciwną do wskazanej liczby, należy ją
pomnożyć przez –1. Np. liczbą przeciwną do 2 jest –2,
liczbą przeciwną do –4 jest 4, liczbą przeciwną do 1 − √2 jest −1 + √2 .